Composite multiscale coherence and application to functional corticomuscular coupling

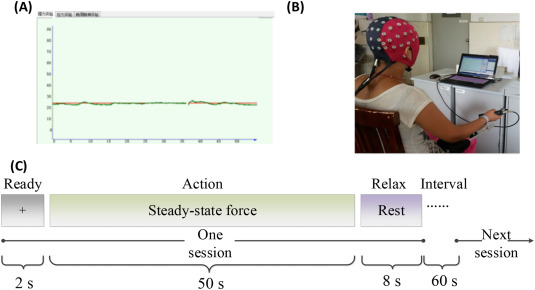
Xiaoling Chen, Ying Liu, Shengcui Cheng, Tingting Shen, Huipeng Gao, Peiguo Hou, Ping Xie

Abstract

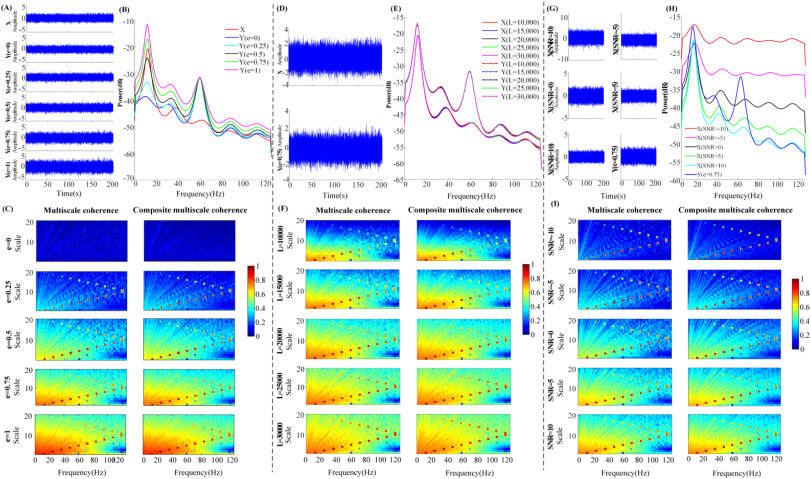
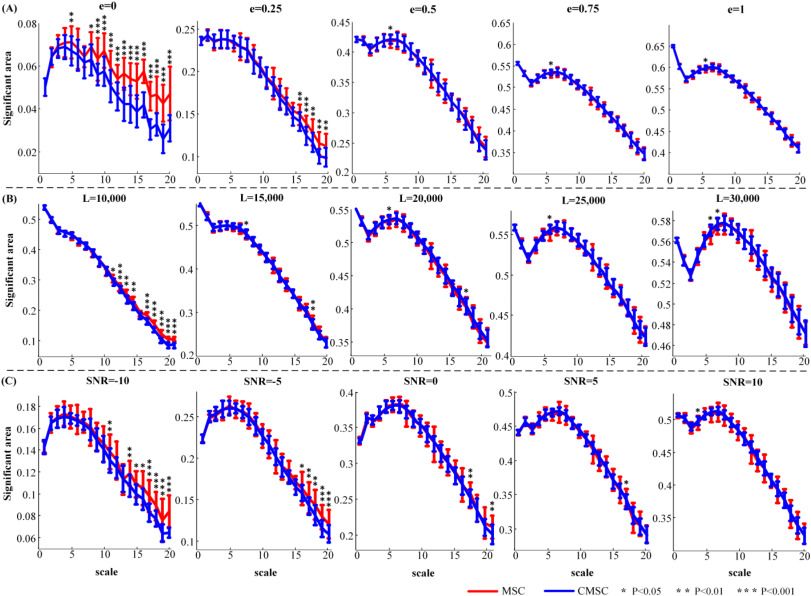
Though coherence, a classical method to describe the linear correlation between two time series, has wide-ranging applications, from economics to neuroscience, it fails to illustrate the inherently multi-time scales-based correlations. In this paper, we proposed a multiscale-like coherence model, defined as composite multiscale coherence (CMSC) by combining the kth coarse-grain processing with the coherence. We made a comparison with the multiscale coherence (MSC) with coarse-grain process in numerical data to compare the sensitivity profiles to the coupling strength, data length and white Gaussian noise. After that, we applied the proposed model to explore the functional corticomuscular coupling (FCMC) by analyzing the correlation between the EEG and EMG signals. Simulation results reflected that the CMSC method were sensitive to the coupling strength, data length and the white Gaussian noise, and presented more stability along the time scale compared to the MSC method. Our application of CMSC methods on the EEG and EMG signals indicated that the FCMC was of multi-time scale characteristics and higher coherence mainly consisted in the alpha and beta bands at about scale 10, though significant area showed a gradual decline with the scale increasing. Further comparison indicated that both models are equally effective to describe the multiscale characteristics of the FCMC at lower time scales, while some differences emerge at the high time scales. Both simulation and experimental data demonstrate the effectiveness of the proposed multiscale-like model to describe the multiscale correlation between two time series. This study extends the relative researches on the FCMC to the multi-time scale.

摘要

相干性是描述两个时间序列之间线性相关性的经典方法，在经济学和神经科学等领域有着广泛的应用，但它无法说明基于多时间尺度的内在相关性。在本文中，我们提出了一种类似于多尺度的相干性模型，通过将第 k 个粗粒度处理与相干性相结合，定义为复合多尺度相干性（CMSC）。我们在数值数据中将其与带粗粒度处理的多尺度相干性（MSC）进行了比较，以比较其对耦合强度、数据长度和白高斯噪声的灵敏度曲线。之后，我们应用所提出的模型，通过分析脑电图和肌电信号之间的相关性来探索皮质肌肉功能耦合（FCMC）。仿真结果表明，CMSC方法对耦合强度、数据长度和白高斯噪声都很敏感，而且与MSC方法相比，在时间尺度上更稳定。我们在脑电图和肌电信号上应用 CMSC 方法的结果表明，FCMC 具有多时间尺度的特征，较高的一致性主要集中在尺度 10 左右的阿尔法和贝塔波段，但显著区域随着尺度的增大而逐渐减小。进一步的比较表明，在低时间尺度上，两种模型对描述 FCMC 的多尺度特征同样有效，而在高时间尺度上则出现了一些差异。模拟和实验数据都证明了所提出的类多尺度模型能有效地描述两个时间序列之间的多尺度相关性。这项研究将 FCMC 的相关研究扩展到了多时间尺度。